平成30年(2018年)3月6日実施、北海道公立高校入試の解説になります。
問題は、北海道教育委員会のサイトからダウンロードできます。
また、予想最低点など各種情報は道コン事務局のサイトに詳しく掲載されています。
今年度の数学は奇をてらった難問はなく、出題の傾向はオーソドックスなものでした。したがって、過去問をやり尽くした人にとっては「新傾向だ」と感じるような問題は、ほとんどなかったと思います。また、解くべき問題を手堅く解いた人は、目標とする点数を超えられるような作りだったとも言えます。
それでは解説に移ります!
急ぎで作成のため、手書きの図であることをお許しください!
【★★★★ 難しい│50点以上を目指す人】
【★★★☆ やや難しい│40点以上を目指す人】
【★★☆☆ 標準│30点以上を目指す人
【★☆☆☆ 易しい│20点以上を目指す人】
大問1(裁量はナシ)
いずれも教科書基礎レベルの出題でした。ミスなく満点を取りたいですね。
| 問1 | ★☆☆☆(1)正負の数 計算 ★☆☆☆(2)正負の数 計算 ★☆☆☆(3)平方根 計算 |
| 問2 | ★☆☆☆ 文字式への代入 |
| 問3 | ★☆☆☆ 1次関数のグラフの式 |
| 問4 | ★☆☆☆ 連立方程式 計算 |
| 問5 | ★☆☆☆ 三平方の定理 計算 |
| 問6 | ★☆☆☆ 球の表面積 |

大問2(裁量:大問1)
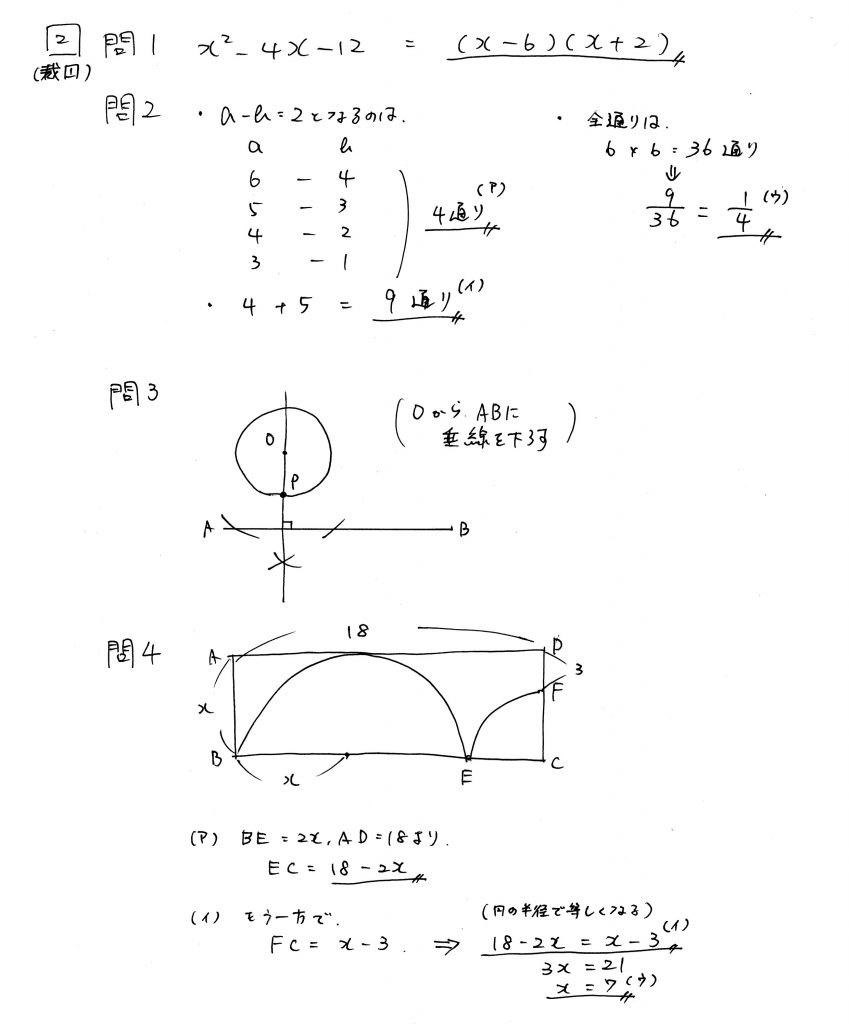
問2の作図は「面積が最小」という図のイメージができれば、作図は簡単。
三角形の面積は、底辺と高さに着目することが攻略のカギとなります。
問4の方程式文章題は、図に長さを書き込めれば、目で見て理解できます。
練習から図形を書いて、そこに長さを書き込むといった練習をすれば攻略できます。
(フリーハンドで、サッと図を書くことをオススメします)
| 問1 | ★☆☆☆ 因数分解 |
| 問2 | ★☆☆☆ 確率 サイコロ |
| 問3 | ★★☆☆ 作図 垂線の利用 |
| 問4 | ★★☆☆ 方程式文章題 図形の応用 |
大問3(裁量:大問2)
【中1:資料の活用】や【中3:標本調査】といった単元は、あまり難しくは出題されません。
今回出題されたような、教科書の基本通りの問題が解ければ、対策は十分でしょう。
問2が記述で説明する形となっていますが、過去問や道コンでもよく出題されるパターンです。
| 問1 | ★☆☆☆ 資料の活用 相対度数 |
| 問2 | ★★☆☆ 資料の活用 中央値 |

大問4(裁量:大問3)
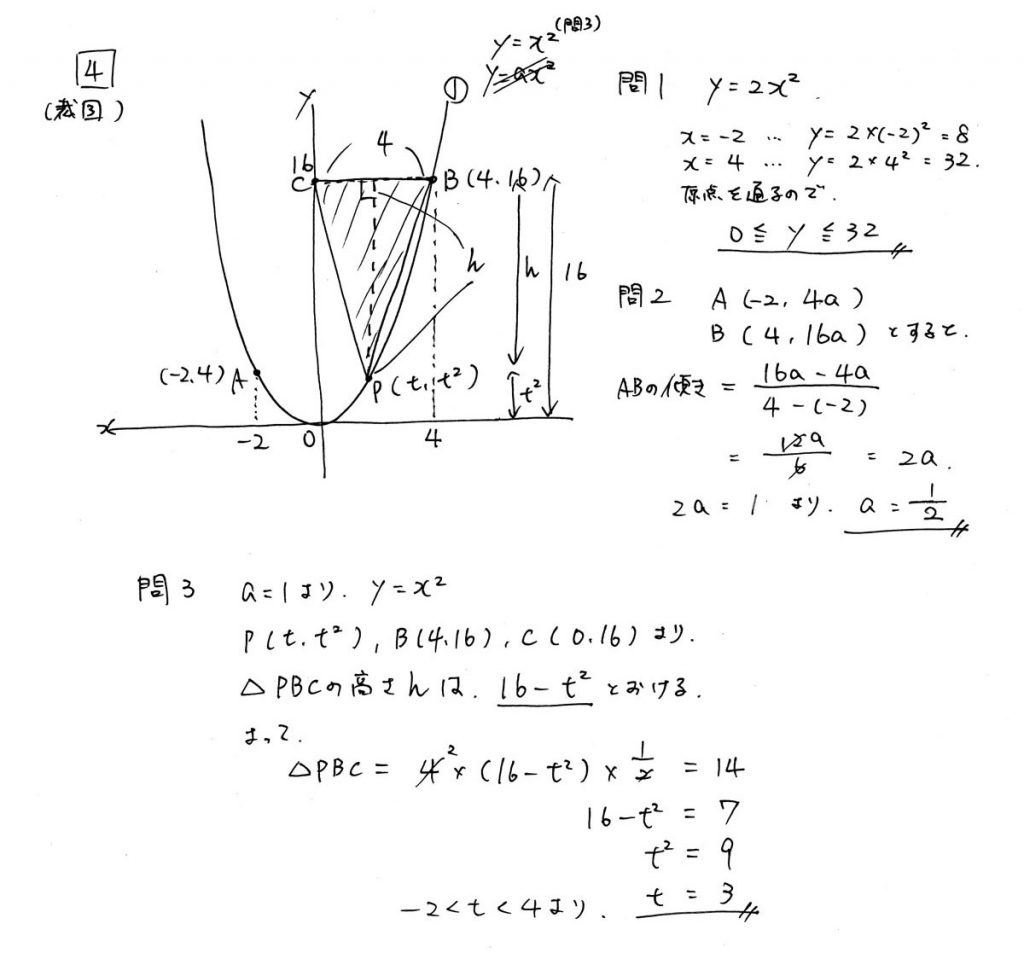
問2は「文字で座標をあらわす」というテクニックが必要です。
y=ax^2に点A・Bのx座標を代入して、aを使って座標をあらわせば、後は解くだけです。
問3も同様に「文字で座標をあらわす」ことができれば、式が立てられます。
点Pの座標を(t,t^2)とあらわせば、三角形の公式に当てはめるだけです。
| 問1 | ★☆☆☆ 二次関数 変域 |
| 問2 | ★★☆☆ 二次関数 1次関数の傾き |
| 問3 | ★★★☆ 二次関数 面積と座標 |
大問5(裁量:大問4)
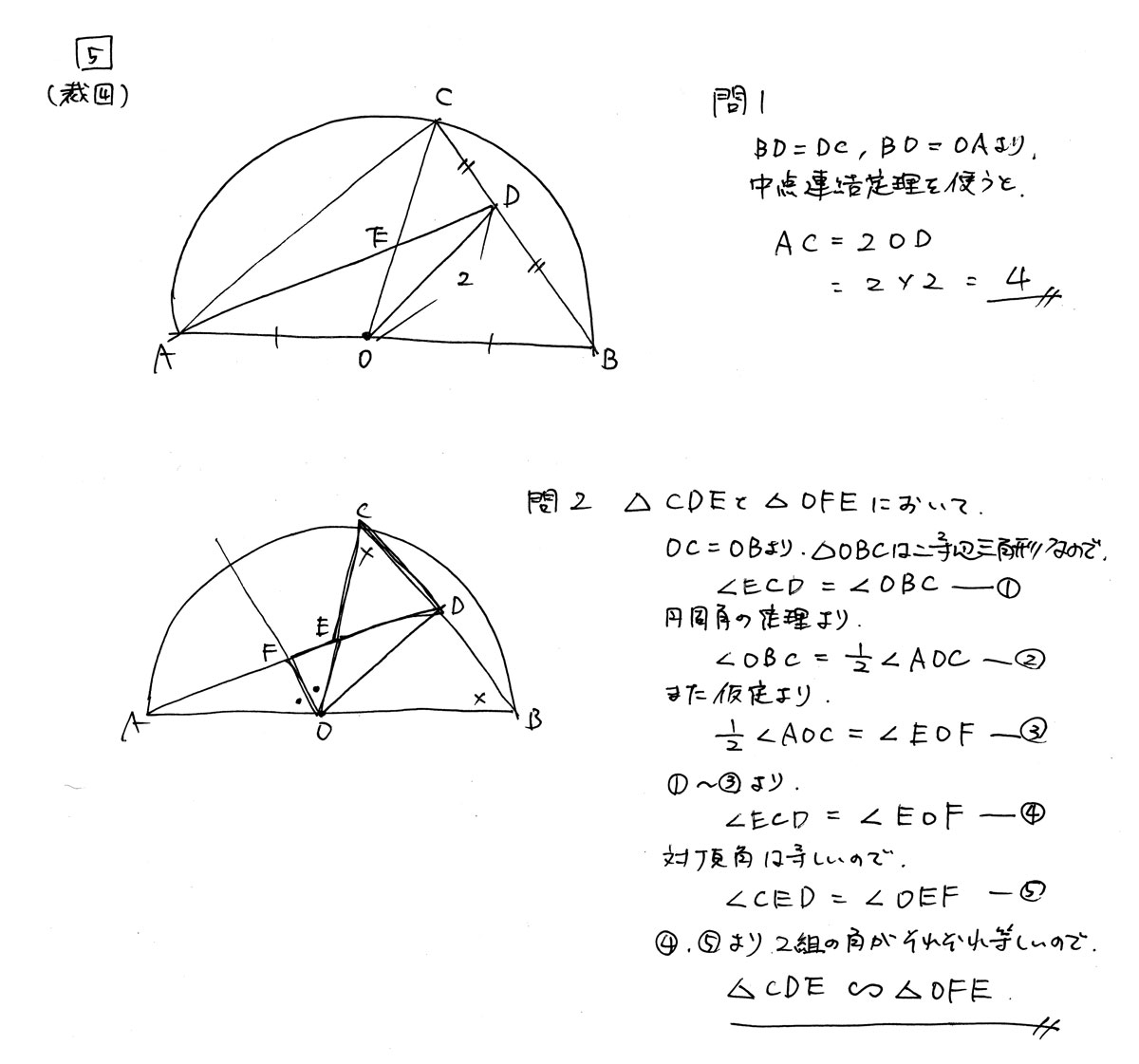
問1は、中点連結定理に当てはめられれば、暗算でも答えをだせます。
「BD=DC」という仮定を見た瞬間に、ピン!ときてほしいところですね。
問2は、等しい角度を順につなげていくところがポイント。
わかっていても、上手くまとめて書けなかった人もいたのではないでしょうか。
「円の半径から生まれた二等辺三角形」を活用する問題が多いので、
円周角だけにとらわれず、円の基本的な性質に目を向けるようにしましょう。
| 問1 | ★★☆☆ 中点連結定理 |
| 問2 | ★★★☆ 相似の証明 円周角を利用 |
裁量:大問5(標準はナシ)
問1は、
図におこせば規則性の問題の中ではシンプルに解ける出題でした。
(1)は、n=2・n=3・n=4と書き出す中で、
いかにnを規則性の中に当てはめられるかが、ポイントとなります。
日頃から、図や表でまとめる練習が必要でしょう。
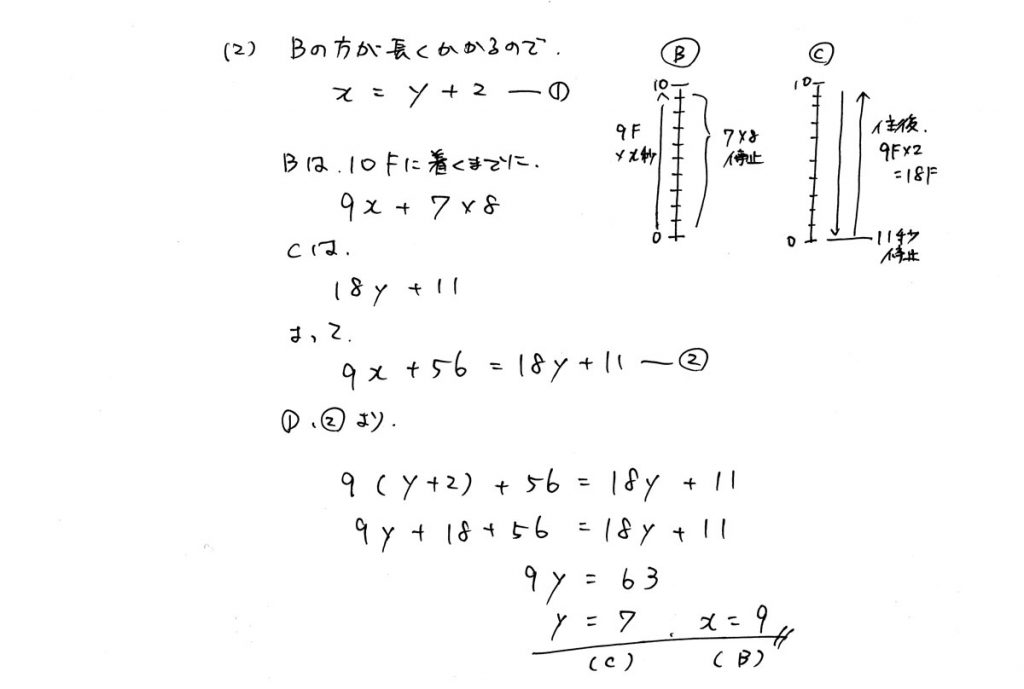
(2)は、(1)で規則性をあらわすことができていれば、
意外とあっけなく式が立てられたはずです。
(1)を乗り越えられたかどうかが、勝負の分かれ道でしたね。
| 問1 | ★★★☆(1)規則性 文字で時間をあらわす ★★★☆(2)規則性 方程式の文章題 |

―――
問2は、
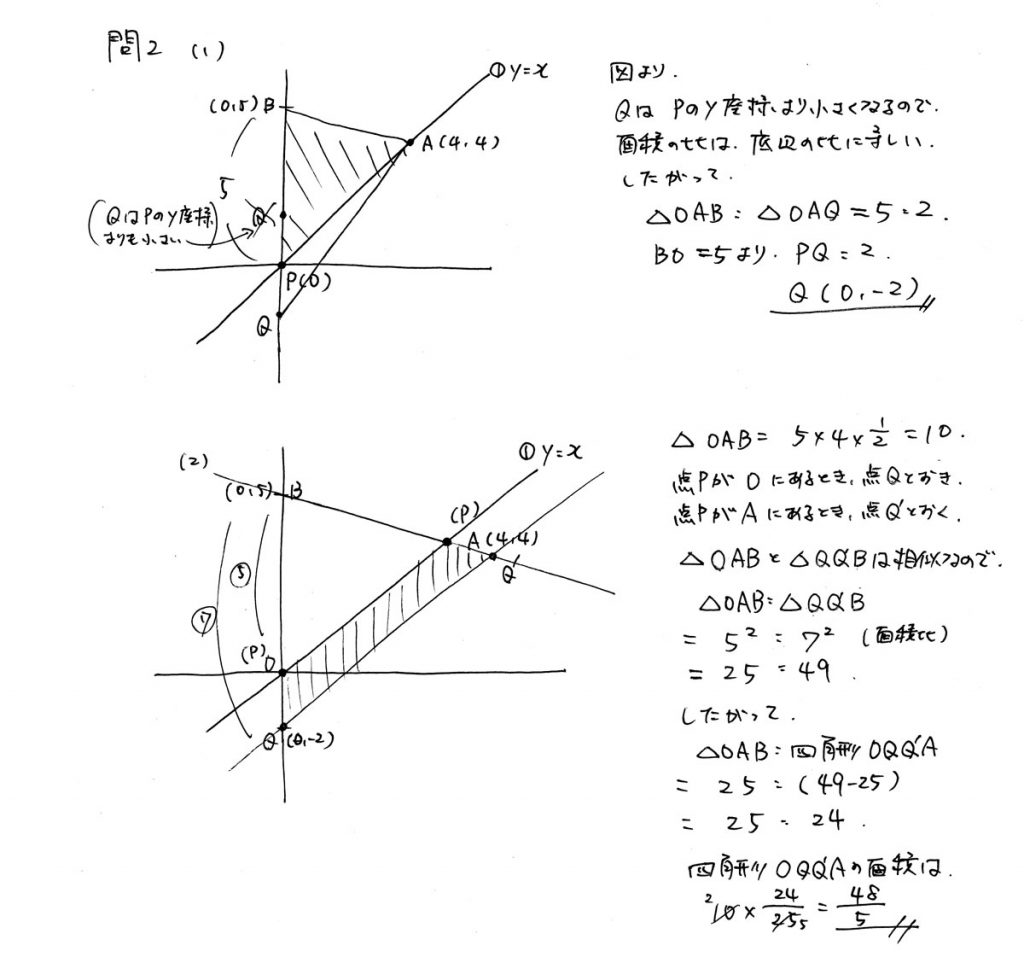
BPの延長線上に点Qがあり、それが面積比5:2になるといった仮定を、
いかにして図にあらわせるかが難しい問題でした。
(1)は、図の状態さえ書き出せれば、計算自体は難しくありません。
△OAB(△PAB)と、△OAQ(△PAQ)において、
高さが共通となるので、底辺の長さの比がそのまま面積比となります。
(2)の図の状態は、(1)が出来ていれば、比較的書きやすいはずです。
相似な図形が生まれるので、
相似比 → 長さの比 → 面積比(比を2乗)とつなげて活用します。
(1)の長さの比の活用と、(2)の相似比の活用を混同する人が多いので、
問題による使い分けが必要となる良問だと思います。
| 問2 | ★★★☆(1)座標と面積比 Qの座標 ★★★★(2)座標と面積比 動点と面積 |
―――
問3は、
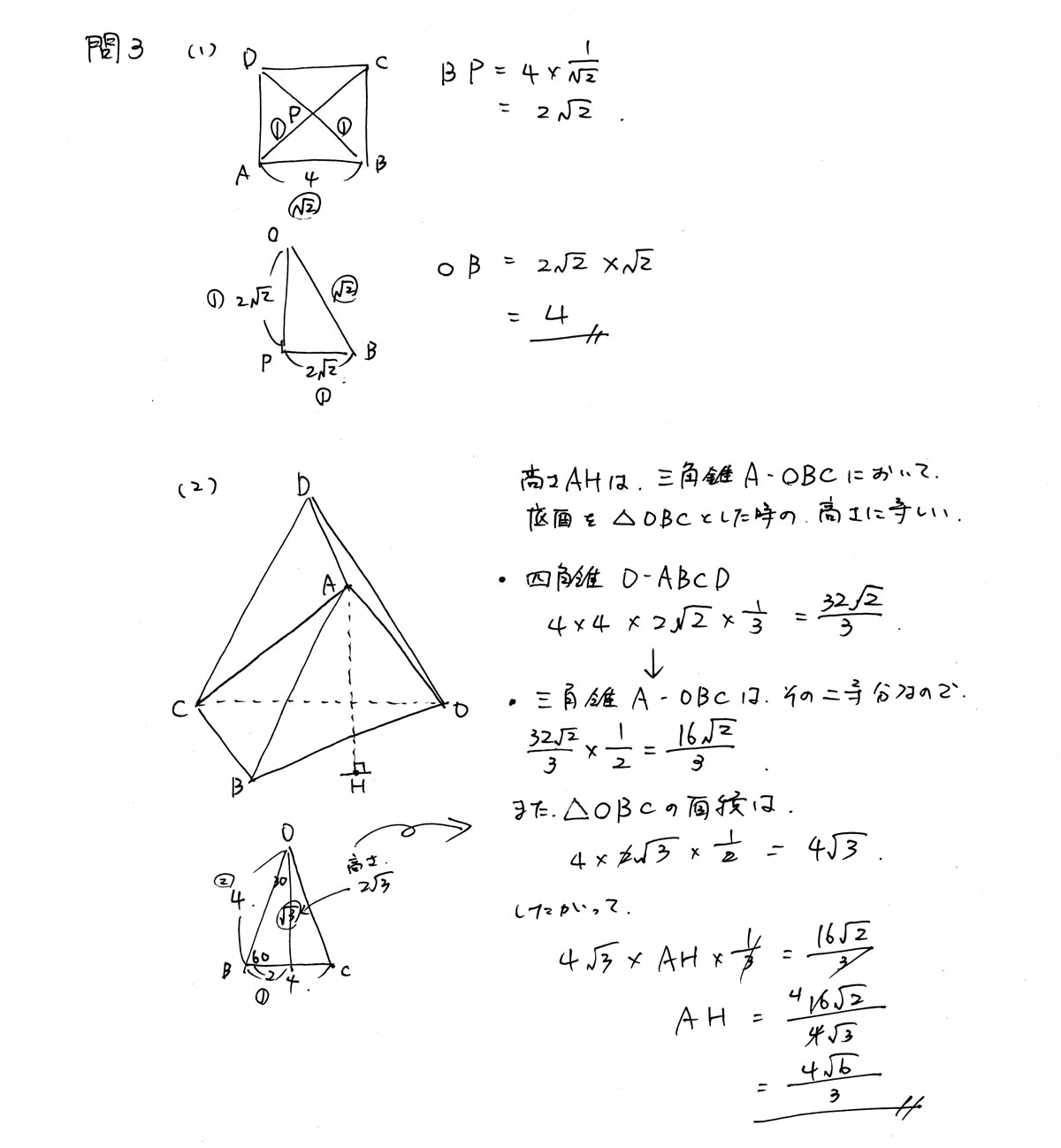
(1)は(2)のヒントとなる、出題者の優しさが感じられる問題でした。
(2)は、ある底面を基準に体積を出しておき、
もう一方の底面から体積を求めることで、高さを導くという、典型的なパターン。
典型的ではあるのですが、四角錐を二等分して考える点や、
高さAHが宙に浮いている点が図のイメージをややこしくしており、
制限時間内に解き切るのは、なかなか難しかったのではないでしょうか。
こちらも程よい難しさの良問だと思います。
マスターしておけば、来年度以降の他の問題にも応用することができるはずです。
| 問3 | ★☆☆☆(1)三平方の定理 長さを求める ★★★★(2)三平方と体積 高さを求める |
以上です。
急ぎで作ったもので、わかりにくい点・見にくい点、はたまた間違いなどがあるかもしれませんが、その際は優しくご指摘いただけるとありがたいです。来年以降の受験生の力となれれば幸いです。


